Reinforcement Learning for Cryptocurrency Portfolio Management
Deep reinforcement learning framework for dynamic cryptocurrency portfolio optimization comparing value-based (DQN, DDQN) and policy gradient (REINFORCE) agents against classical baselines. DDQN outperforms passive strategies with 190.77% returns on a 646-day out-of-sample test.
The Challenge: Can Deep RL Learn Profitable Allocation Strategies?
The cryptocurrency market has grown from a niche experiment to a multi-trillion-dollar asset class, bringing unique challenges for portfolio management: daily volatility that frequently exceeds traditional equity markets, continuous 24/7 trading across fragmented exchanges, and cross-asset correlations that shift substantially between bull and bear regimes.
Deep reinforcement learning has demonstrated strong performance in sequential decision-making domains, prompting researchers to explore its application to financial portfolio management. The portfolio management problem—dynamically allocating capital across multiple assets to maximize risk-adjusted returns—naturally maps to a Markov Decision Process. Unlike supervised learning approaches that predict returns and then optimize, RL directly learns the allocation policy end-to-end, potentially capturing complex temporal dependencies and trading off immediate costs against future opportunities.
This research investigates whether deep RL agents can learn profitable portfolio allocation strategies that outperform classical approaches under realistic trading conditions. Developed as part of EN605.741 Reinforcement Learning at Johns Hopkins University, we implement a comprehensive experimental framework addressing practical challenges: variable asset universes, realistic transaction costs, and fair comparison across different algorithmic paradigms.
Methodology: Rigorous MDP Formulation
State Space
At each trading day $t$, the state consists of a per-asset historical observation tensor and previous portfolio weights:
\[\mathbf{X}_t \in \mathbb{R}^{A_t \times 4 \times 60}\]where $A_t$ denotes the number of tradable assets (varying between 8-35 daily), 4 channels capture Close, High, Low, and Volume data, and 60 represents the lookback window in days. The inclusion of previous weights enables agents to internalize turnover costs.
Action Space: Two Paradigms
Discrete (DQN/DDQN): A 70-action delta-based catalog including hold actions, exposure adjustments ($\pm5\%$, $\pm10\%$, $\pm15\%$ to top-K assets), rotation actions transferring weight between asset pairs, and rebalancing to equal or market-cap weights. This preserves portfolio continuity and enables context-dependent feasibility learning.
Continuous (REINFORCE): Direct parameterization of portfolio weights via Dirichlet distribution with concentration parameters $\boldsymbol{\alpha} = \text{softplus}(\text{logits}) / \tau$, enabling fully continuous allocation optimization.
Reward Function
The reward incorporates realistic transaction costs matching centralized exchange fee structures:
\[r_t = \log\left(1 + \mathbf{w}_t^\top \mathbf{R}_{t+1}\right) - c \cdot \lVert \mathbf{w}_t - \mathbf{w}_{t-1} \rVert_1\]where $c = 0.001$ (10 basis points per unit turnover). Critically, forward returns $\mathbf{R}_{t+1}$ are never observed at decision time—they compute realized rewards only after actions are taken.
Constraints
All portfolios must satisfy:
- Long-only: $w_t^{(i)} \geq 0$ (no short selling)
- Fully invested: $\sum_{i=1}^{A_t} w_t^{(i)} = 1$ (no cash holdings)
- Turnover limit: $\lVert \mathbf{w}_t - \mathbf{w}_{t-1} \rVert_1 \leq 0.30$ (daily cap)
The fully-invested constraint forces agents to maintain cryptocurrency exposure rather than trivially holding cash, ensuring fair comparison against crypto benchmarks.
Agent Architectures
Deep Q-Network (DQN) & Double DQN
Value-based agents using canonical padding to handle variable universe sizes. Each of 37 unique assets receives a fixed canonical position, with observations zero-padded and projected through a learned linear layer to 256-dimensional embeddings. The Q-network is a 3-layer MLP (512→256→70) with experience replay, $\epsilon$-greedy exploration, and target network updates.
DDQN differs in the TD target computation:
\[Q_{\text{target}} = r + \gamma \, Q_{\text{target}}(s', \underset{a'}{\operatorname{argmax}} \, Q_{\text{online}}(s', a'))\]This decouples action selection from evaluation, reducing the overestimation bias that can destabilize learning in non-stationary environments.
REINFORCE & REINFORCE+Baseline
Policy gradient agents with a GRU encoder processing the 60-day sequence, outputting per-asset logits converted via masked softmax to portfolio weights. When sampled allocations violate constraints, the environment projects them onto the feasible set.
REINFORCE+Baseline adds a value head $V_\phi(s_t)$ sharing the GRU encoder, using advantage estimation $A_t = G_t - V_\phi(s_t)$ for variance reduction.
Classical Baselines
- Equal Weight (1/N): Uniform allocation—remarkably competitive by avoiding estimation error
- Market Cap Weight: Proportional to market capitalization, mimicking index funds
- Mean-Variance Optimization: Markowitz optimization with Ledoit-Wolf shrinkage for covariance estimation
Results: 646-Day Out-of-Sample Test
We evaluate all strategies on held-out test data from January 2024 through October 2025.
Test Set Performance
| Agent | Return (%) | CAGR (%) | Sharpe | Sortino | Max DD (%) | Turnover (%) |
|---|---|---|---|---|---|---|
| Mean-Variance | 366.54 | 139.07 | 1.640 | 1.691 | 39.96 | 13.50 |
| DDQN | 190.77 | 82.95 | 1.247 | 1.298 | 49.93 | 6.28 |
| Equal Weight | 168.50 | 74.88 | 1.217 | 1.250 | 48.87 | 0.25 |
| REINFORCE+Baseline | 167.37 | 74.46 | 1.202 | 1.235 | 49.26 | 0.35 |
| REINFORCE | 161.84 | 72.41 | 1.195 | 1.220 | 48.83 | 0.88 |
| Market Cap | 159.30 | 71.46 | 1.240 | 1.298 | 44.17 | 0.34 |
| DQN | 135.05 | 62.20 | 1.092 | 1.114 | 48.99 | 5.67 |
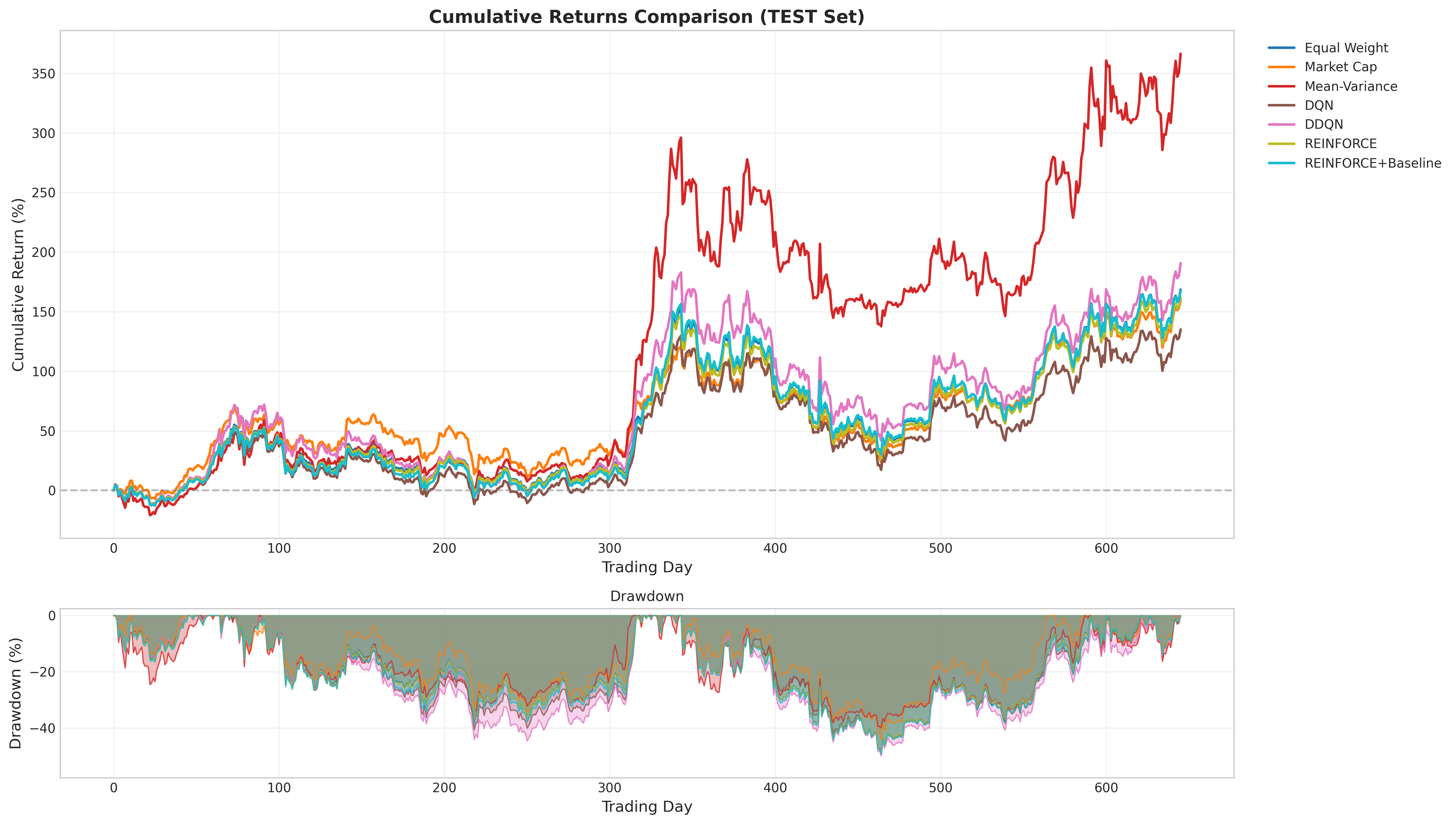Cumulative returns over the test period. Mean-Variance achieves 366% return; DDQN (190.77%) outperforms all passive baselines. REINFORCE+Baseline (167.37%) nearly matches Equal Weight with minimal turnover.
Key Findings
1. DDQN Outperforms Passive Baselines: Among RL agents, DDQN achieved 190.77% return—outperforming Equal Weight (168.50%) and Market Cap (159.30%) with moderate turnover (6.28%). Double Q-learning’s theoretical motivation proved effective: decoupling action selection from evaluation reduces optimistic bias in non-stationary markets.
2. Value-Based vs. Policy Gradient Tradeoffs: Standard DQN achieved only 135.05% despite similar architecture, highlighting DDQN’s stability advantage. Policy gradient agents performed competitively under deterministic evaluation—REINFORCE+Baseline reached 167.37% with turnover of just 0.35%, demonstrating that learned allocation preferences require appropriate inference-time behavior.
3. Classical Optimization Remains Formidable: Mean-Variance’s dominance (366.54%) reflects favorable market conditions where momentum signals in rolling return estimates carried predictive information. However, MVO’s edge may not generalize to mean-reverting or crash regimes.
4. Action Space Design Matters: The gap between DDQN (190.77%) and REINFORCE+Baseline (167.37%) suggests delta-based discrete actions provide structural advantages for constrained portfolio optimization by enabling incremental adjustments without dramatic position changes.
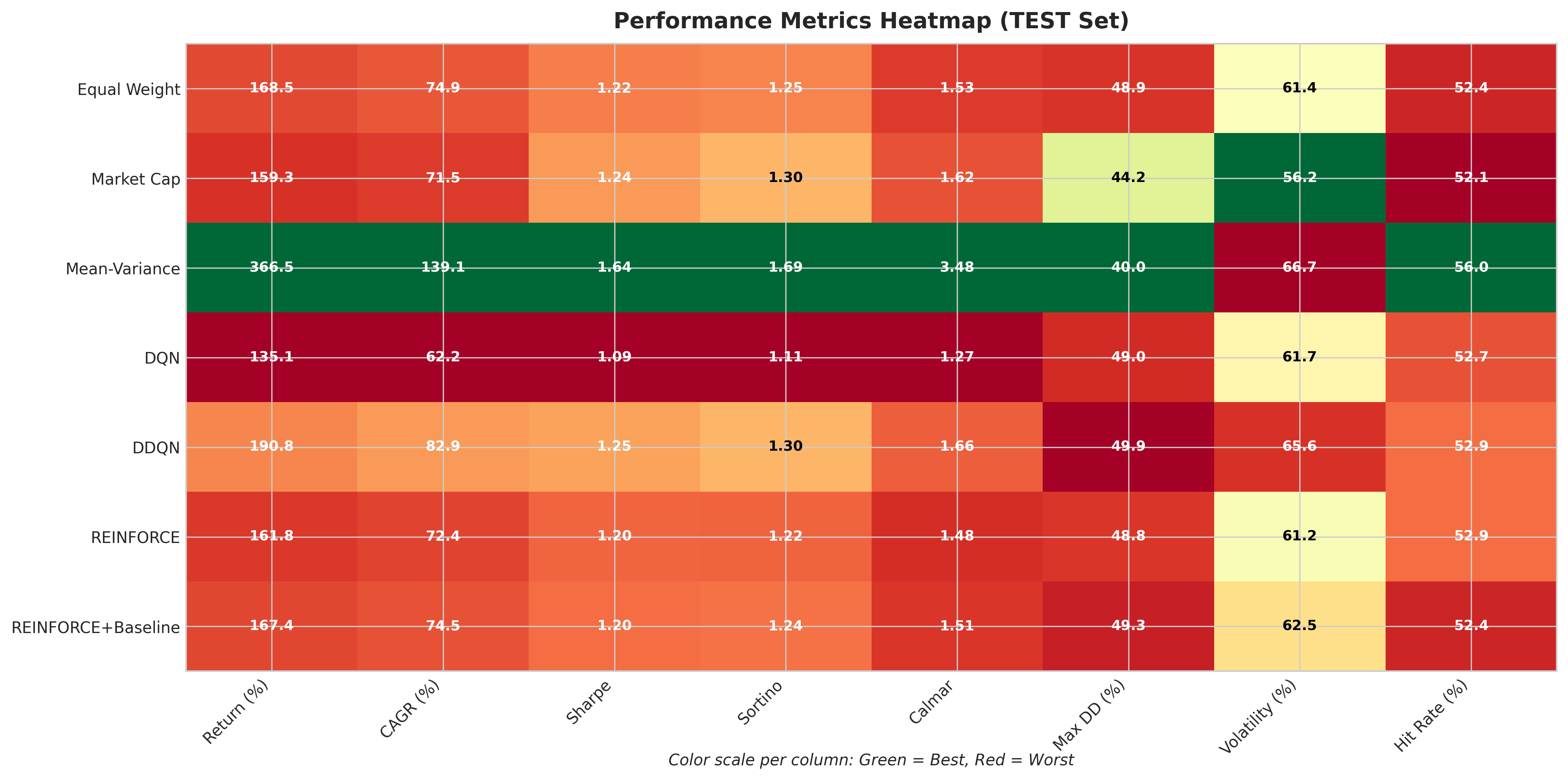Comprehensive metrics heatmap showing performance across return, risk-adjusted, and drawdown measures.
Technical Contributions
Variable Universe Environment
A portfolio management environment handling dynamic asset membership with monthly reconstitution, cold-start eligibility rules (60 days of clean data required), and automatic weight redistribution when assets exit. We release a frozen dataset export enabling exact reproduction.
Delta-Based Discrete Action Space
A 70-action catalog of relative portfolio adjustments for DQN agents, preserving portfolio continuity and enabling context-dependent feasibility learning through penalty-based constraint enforcement.
Canonical Padding for Variable-Size Observations
A scheme mapping variable-size observations to fixed-dimensional representations while preserving asset identity essential for Q-value learning.
Rigorous Evaluation Framework
Regime-diverse validation across five market conditions (crypto winter, COVID crash, bull market, bear market, consolidation) prevents overfitting hyperparameters to a single regime. Bayesian optimization via Optuna searches 50 configurations per agent.
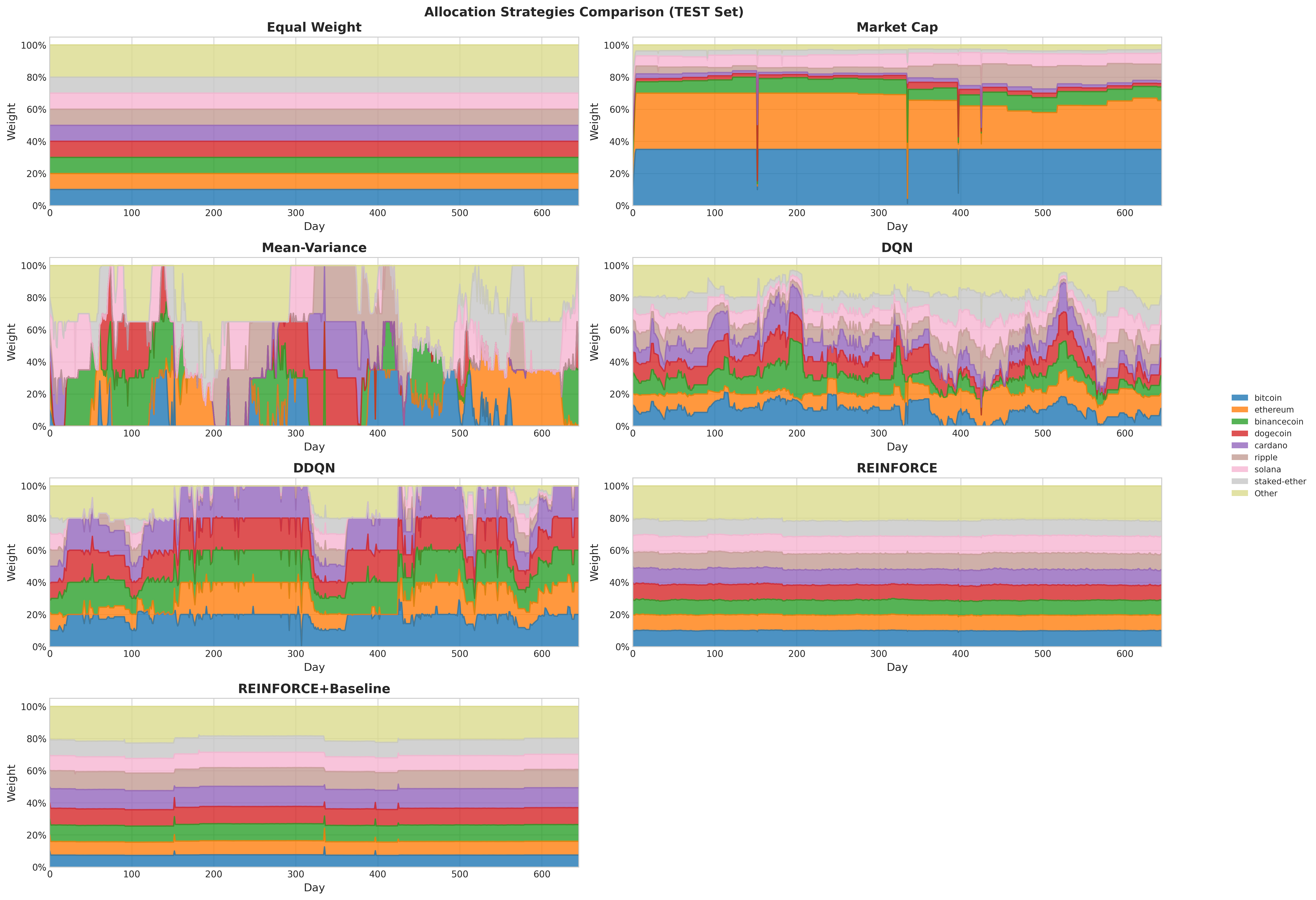Allocation strategies across agents. Mean-Variance exhibits dynamic reallocation with concentrated positions. DDQN shows moderate rebalancing. REINFORCE variants display stable allocations under deterministic evaluation.
Discussion: Interpreting the Results
The dichotomy between value-based and policy gradient methods reveals important lessons about action space design. DDQN’s success demonstrates that value-based RL can learn meaningful allocation policies when equipped with appropriate discrete actions. The delta-based catalog enabled incremental adjustments while double Q-learning provided stability.
Policy gradient agents learned meaningful allocation preferences, but realizing this potential required deterministic evaluation using the Dirichlet mean ($\alpha_i / \sum_j \alpha_j$) rather than sampling. This produces smooth weight proposals that naturally satisfy turnover constraints—a crucial insight for deployment.
Mean-Variance optimization’s dominance reflects both favorable market conditions and sample efficiency advantages. MVO directly estimates sufficient statistics from historical data and solves a closed-form optimization, using data efficiently compared to model-free RL that must rediscover statistical relationships through gradient descent.
Future Directions
Several promising extensions could build on this foundation:
- Deterministic policy gradients (DDPG, TD3): A natural middle ground between discrete and sampled continuous actions
- Transformer architectures: Cross-asset attention for implicit correlation modeling, combining MVO’s correlation reasoning with deep learning flexibility
- Extended regime evaluation: Testing across sustained bear markets and crash periods
- Online learning: Adaptive approaches that evolve with changing market dynamics
Resources
Research Paper: Download Complete Paper (PDF)
Code Repository: github.com/josemarquezjaramillo/crypto-rl-portfolio
Technologies: PyTorch, Optuna, pandas, NumPy, PostgreSQL, SQLAlchemy, pytest, matplotlib, seaborn
Citation:
Márquez Jaramillo, J. & Hawks, T. (2025). Reinforcement Learning for
Cryptocurrency Portfolio Management. Johns Hopkins University,
EN605.741 Reinforcement Learning.
This project demonstrates that careful implementation of established RL algorithms can yield portfolio strategies that outperform passive investment approaches. The gap between research benchmarks and practical deployment is narrower than sometimes claimed—DDQN’s outperformance of passive baselines validates deep RL’s potential in constrained financial optimization. Completed as coursework for EN605.741 Reinforcement Learning at Johns Hopkins University.